Strength calculations of the double spring
At the request of OOO "NPC" Spring "have been carried out strength calculations on dual spring design scheme and drawings provided by the customer.
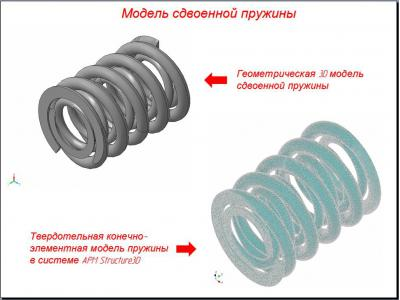
The purpose of the calculation is to determine the maximum stresses arising in the spring body at its crimping to a static load to the contact turns. Determining a sufficient yield strength of the spring material in order to withstand at least 500 000 cycles. Design and analysis of layer model proposed in the specifications of the spring.
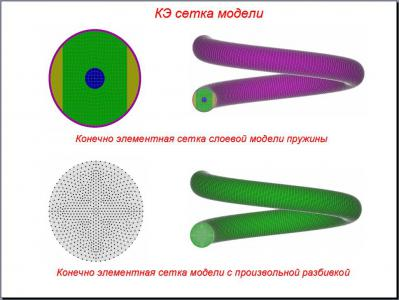
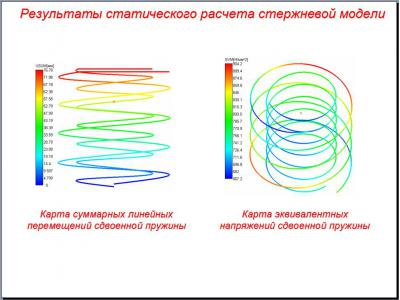
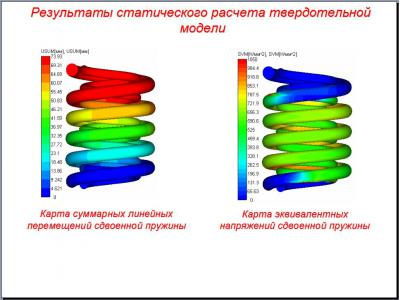
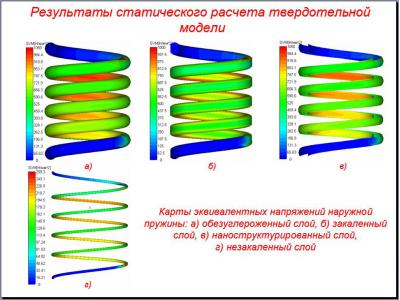
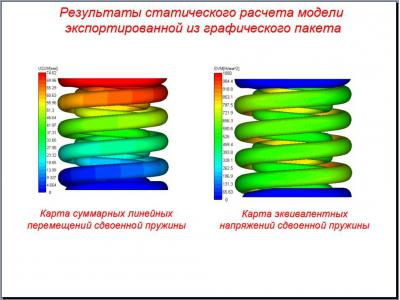
To construct a computational model of the spring package used tools APM Structure3D and APM Studio. The first and second kinematic model built by ejecting a pre-prepared (broken into finite elements) of the section of five turns with predetermined, constant spacing. In these models, the extreme (outside of) the spring windings (upper and lower) are not formed, due to high complexity problem. Construction of the third model was carried out by export models built in Pro / Engineer, in APM Studio package by step format. In this extreme case (outside) of the spring coils are formed, but the construction of the layered model is thus not possible. In addition to carrying out the verification tests built core models of these springs.
Table 1 Parameters sectional springs models
model | The number of degrees of freedom (nodes) | The number of finite elements in section | |
- triangles | - quads | ||
19 mm (layers) | 3341679 (1113893) | 48 | 704 |
27 mm (layers) | 2089419 (696,473) | 48 | 704 |
Dual 19-27 mm (layers) | 5431098 (1,810,366) | 96 | 1408 |
19 mm (arbitrary) | 3307095 (1,102,365) | 1464 | 0 |
27 mm (arbitrary) | 2067795 (689,265) | 1464 | 0 |
Dual (19-27 mm) (arbitrary) | 5374890 (1,791,630) | 2928 | 0 |
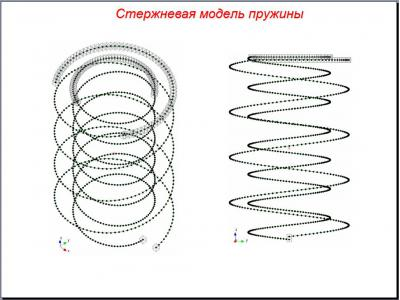
Modeling of the spring to compression static load was performed on five models:
- finite-element layered with a section breakdown (extreme coils are not formed);
- finite element with an arbitrary cross-section breakdown (extreme coils are not formed);
- finite element with an arbitrary, automatically generated, the grid (last coils formed);
- rod.
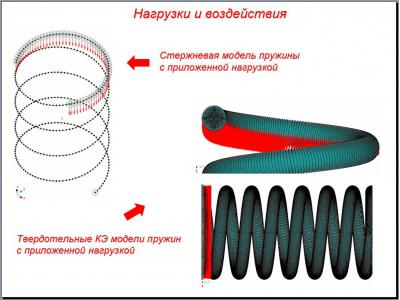
The magnitude of the external load was taken, according to the statement with the drawings provided by the customer. For it is the inner spring F 1 = 8.88 kN for outdoor F 2 = 819.084 kN, for the dual F 3 = 27.964 kN.
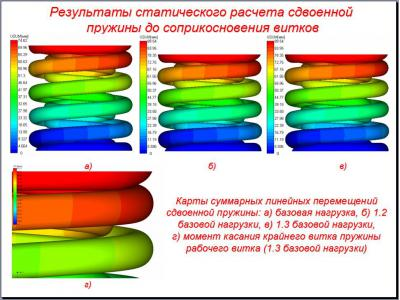
The analysis of stress-deformed state of the spring when it turns before contact crimping was performed for model constructed in Pro / Engineer and exported in APM Studio package via step size, followed by automatic generation of finite element mesh.
Because the exact definition of the time of contact of turns is difficult, the procedure used gradually increasing the external load (in 10% increments) to a maximum value. In this case, the reference point of the working coil tangency determined visually, and the load at which the touch is in a range between two loaded.
Table 2 - Loadings
number | Name of loading | load Description |
1 | base load | Regulatory static load (depending on the type of spring F 1 = 8.88 kN, F 2 = 819.084 kN, F 3 = 27.964 kN |
2 | 1.1 base | Increased by 10% the static load normative |
3 | 1.2 base | Increased by 20% the static load normative |
4 | 1.3 base | Increased by 30% regulatory static load |
5 | 1.4 base | An increase of 40% regulatory static load |
6 | 1.5 base | Increased by 50% the static load normative |
7 | 1.6 base | Increased by 60% the static load normative |
The results of structural analysis
Table 3 - Summary of the results of calculation on the static load springs
number | Name parameter | external spring | internal spring | dual spring |
1 | Static force, N | 19084 | 8880 | 27964 |
2 | The magnitude of the axial precipitation, mm (Engineering calculation) | 75.32 | 75.14 | 75.26 |
3 | The magnitude of the axial precipitation, mm (Rod model) | 76.83 | 76.64 | 76.78 |
4 | The magnitude of the axial precipitation, mm (Layer model) | 77.38 | 76.24 | 73.93 |
5 | The magnitude of the axial precipitation, mm (Arbitrary split) | 77.46 | 76.99 | 77.06 |
6 | The magnitude of the axial precipitation, mm (Automatic split) | 75.47 | 74.58 | 74.62 |
Table 24 - Results of calculation of the dual contact spring turns to
number | Name uploading | The magnitude of the axial spring precipitation, mm | The presence of turns of contact |
1 | base load | 74.62 | - |
2 | 1.1 base | 82.08 | - |
3 | 1.2 base | 89.54 | - |
4 | 1.3 base | 97.01 | + |
5 | 1.4 base | 104.5 | + |
6 | 1.5 base | 111.9 | + |
7 | 1.6 base | 119.4 | + |