PHASE III MATHEMATICAL TECHNOLOGY

| COURSE BY MATHEMATICAL TECHNOLOGY ON APPLICATION |
101 SYMBOLIC GEOMETRY EXAMPLES WITH GEOMETRY EXPRESSIONS Philip Todd |
CALCULUS EXPLORATIONS WITH GEOMETRY EXPRESSIONS HANNAH IRINA LYUBLINSKAYA/ HANNAH VALERIY RYZHIK |
| 101 CONIC SECTIONS EXAMPLES WITH GEOMETRY EXPRESSIONS Philip Todd |
| CONNECTING ALGEBRA AND GEOMETRY THROUGH TECHNOLOGY JIM WIECHMANN |
DEVELOPING GEOMETRY PROOFS WITH GEOMETRY EXPRESSIONS™IRINA LYUBLINSKAYA, VALERIY RYZHIK, DAN FUNSCH |
EXPLORING WITH GEOMETRY EXPRESSIONS IN HIGH SCHOOL MATHEMATICSIAN SHEPPARD |
101 SYMBOLIC GEOMETRY EXAMPLES WITH GEOMETRY EXPRESSIONS(Philip Todd)
INTRODUCTION
EXAMPLE 1: MEDIAN & ANGLE BISECTOR OF A RIGHT TRIANGLEI
EXAMPLE 2: ANGLES AND CIRCLES
EXAMPLE 3: RECTANGLE CIRCUMSCRIBING AN EQUILATERAL TRIANGLE
EXAMPLE 4: AREA OF A HEXAGON BOUNDED BY TRIANGLE SIDE TRISECTORS
INCIRCLES / CIRCUMCIRCLES / EXCIRCLES / AREAS
EXAMPLE 5: CIRCUMCIRCLE RADIUS
EXAMPLE 6: INCIRCLE RADIUS
EXAMPLE 7: INCIRCLE CENTER IN BARYCENTRIC COORDINATES
EXAMPLE 8: HOW DOES THE POINT OF CONTACT WITH THE INCIRCLE SPLIT A LINE
EXAMPLE 9: EXCIRCLES
NAPOLEON’S THEOREM / PYTHAGORAS DIAGRAM
EXAMPLE 10: NAPOLEON’S THEOREM
EXAMPLE 11: AN UNEXPECTED TRIANGLE FROM A PYTHAGORAS-LIKE DIAGRAM
EXAMPLE 12: A PENEQUILATERAL TRIANGLE
EXAMPLE 13: ANOTHER PENEQUILATERAL TRIANGLE
EXAMPLE 14: VON ABUEL’S THEOREM
CIRCLE COMMON TANGENTS
EXAMPLE 15: LOCATION OF INTERSECTION OF COMMON TANGENTS
EXAMPLE 16: CYCLIC TRAPEZIUM DEFINED BY COMMON TANGENTS
EXAMPLE 17: TRIANGLE FORMED BY THE INTERSECTION OF THE INTERIOR COMMON TANGENTS OF THREE CIRCLES
EXAMPLE 18: LOCUS OF CENTERS OF COMMON TANGENTS TO TWO CIRCLES
EXAMPLE 19: LENGTH OF THE COMMON TANGENT TO TWO TANGENTIAL CIRCLES
EXAMPLE 20: TANGENTS TO THE RADICAL AXIS OF A PAIR OF CIRCLES
EXAMPLE 21: THE EYEBALL THEOREM
EXAMPLE 22: A LIMIT POINT ARBELOS
EXAMPLE 23: TWO CIRCLES INSIDE A CIRCLE TWICE THE RADIUS, THEN A THIRD
EXAMPLE 24: A THEOREM OLD IN PAPPUS’ TIME
EXAMPLE 25: ANOTHER FAMILY OF CIRCLES
EXAMPLE 26: ARCHIMEDES TWINS
EXAMPLE 27: BUEHLER’S CIRCLE
EXAMPLE 28: CIRCLE TO TWO CIRCLES ON ORTHOGONAL RADII OF A THIRD
CONICS
EXAMPLE 29: CIRCLE OF APOLLONIUS
EXAMPLE 30: A CIRCLE INSIDE A CIRCLE
EXAMPLE 31: PARABOLA AS LOCUS OF POINTS EQUIDISTANT BETWEEN A POINT AND A LINE
EXAMPLE 32: PARABOLIC MIRROR
EXAMPLE 33: SQUEEZING A CIRCLE BETWEEN TWO CIRCLES
EXAMPLE 34: ELLIPSE AS A LOCUS
EXAMPLE 35: ARCHIMEDES TRAMMEL
EXAMPLE 36: AN ALTERNATIVE ELLIPSE CONSTRUCTION
EXAMPLE 37: “BENT STRAW” ELLIPSE CONSTRUCTION
EXAMPLE 38: ANOTHER ELLIPSE
EXAMPLE 39: SIMILAR CONSTRUCTION FOR A HYPERBOLA
EXAMPLE 40: ELLIPSE AS ENVELOPE OF CIRCLES
EXAMPLE 41: HYPERBOLA AS AN ENVELOPE OF CIRCLES
EXAMPLE 42: HYPERBOLA AS AN ENVELOPE OF LINES
EXAMPLE 43: CURVATURE OF CONIC SECTIONS
MECHANISMS
EXAMPLE 44: A CRANK PISTON MECHANISM
EXAMPLE 45: A QUICK RETURN MECHANISM
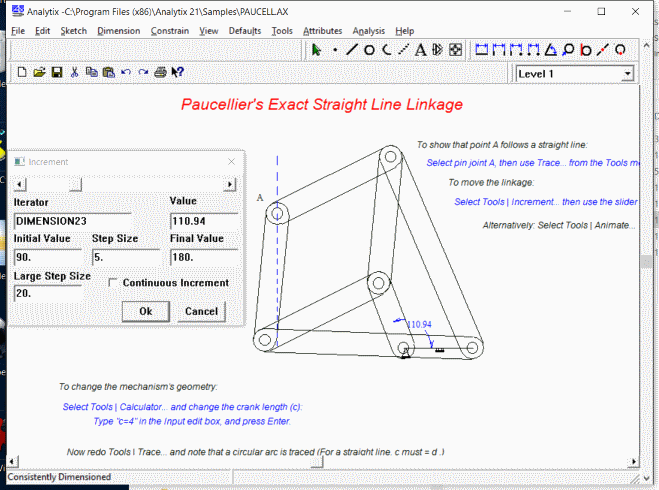
EXAMPLE 46: PAUCELLIER’S LINKAGE
EXAMPLE 47: OFF CENTERED CIRCULAR CAM
EXAMPLE 48: SINUSOIDAL MOTION FROM A RECIPROCATING ROLLER FOLLOWER
EXAMPLE 49: GENERAL DISC CAM WITH A RECIPROCATING ROLLER FOLLOWER
EXAMPLE 50: HARBORTH GRAPH
SPLINE CURVES
EXAMPLE 51: CUBIC SPLINE
EXAMPLE 52: A TRIANGLE SPLINE
EXAMPLE 53: ANOTHER TRIANGLE SPLINE
CAUSTICS
EXAMPLE 54: CAUSTICS IN A CUP OF COFFEE
EXAMPLE 55: A NEPHROID BY ANOTHER ROUTE
EXAMPLE 56: CAUSTIC IN AN ELLIPSE
EXAMPLE 57: COFFEE CUP CAUSTICS REVISITED – FINITE LIGHT SOURCE
EXAMPLE 58: TSCHIRNHAUSEN’S CUBIC
EXAMPLE 59: GENERAL CAUSTIC (PARALLEL RAYS)
EXAMPLE 60: GENERAL CAUSTIC (POINT LIGHT SOURCE)
CURVES
EXAMPLE 61: ROSACE A QUATRE BRANCHES
EXAMPLE 62: OVAL OF CASSINI
EXAMPLE 63: OVAL OF DESCARTES
EXAMPLE 64: PASCAL’S LIMAÇON
EXAMPLE 65: KULP QUARTIC & THE WITCH OF AGNESI
EXAMPLE 66: NEWTON’S STROPHOID
EXAMPLE 67: MACLAURIN’S TRISECTRIX AND OTHER SUCH LIKE
EXAMPLE 68: TRISECTRICE DE DELANGE
EXAMPLE 69: “FOGLIE DEL SUARDI”
EXAMPLE 70: A CONSTRUCTION OF DIOCLETIAN
EXAMPLE 71: KAPPA CURVE
EXAMPLE 72: KEPLER’S EGG
EXAMPLE 73: CRUCIFORM CURVE
EXAMPLE 74: PEDAL CURVE OF A PARABOLA
EXAMPLE 75: NEGATIVE PEDAL CURVE OF A PARABOLA
EXAMPLE 76: CONTRAPEDAL CURVE OF A PARABOLA
EXAMPLE 77: EVOLUTE OF A PARABOLA
EXAMPLE 78: PARALLEL CURVES TO PARABOLAS
EXAMPLE 79: LIMIT OF THE CIRCUMCIRCLE AND EXCIRCLE
FUNCTIONS AND PARAMETRIC CURVES
EXAMPLE 80: INTERSECTION OF TWO TANGENTS TO A QUADRATIC
EXAMPLE 81: TANGENT TO A CUBIC
EXAMPLE 82: AREA UNDER A CHORD OF A PARABOLA
EXAMPLE 83: AREA OF A TRIANGLE FORMED BY A TANGENT TO THE FUNCTION Y =1/X
EXAMPLE 84: ORTHOCENTER OF TRIANGLE DEFINED BY 3 POINTS ON THE FUNCTION Y="1/X
EXAMPLE 86: OFFSET CURVE
EXAMPLE 87: EVOLUTE OF THE LOGARITHMIC SPIRAL
EXAMPLE 88: PEDAL CURVE WHERE THE PEDAL POINT IS ON THE EVOLUTE
MISCELLANEOUS PROBLEMS
EXAMPLE 89: FEYNMAN’S TRIANGLE
EXAMPLE 90: A GENERALIZATION OF FEYNMAN’S TRIANGLE
EXAMPLE 91: MIXTILINEAR INCIRCLES AND EXCIRCLES
EXAMPLE 92: JOINING THE CENTERS OF CIRCLES TANGENT TO 2 SIDES OF A TRIANGLE AND CENTER LYING ON THE THIRD
EXAMPLE 93: MAXIMIZING THE ANGLE FOR A RUGBY KICK
EXAMPLE 94: TRIANGULATION
EXAMPLE 95: AREA OF THE PEDAL TRIANGLE
EXAMPLE 96: FAGNANO’S ALTITUDE BASE PROBLEM
EXAMPLE 97: REGIOMONTANUS’ MAXIMUM PROBLEM
EXAMPLE 98: EULER’S TETRAHEDRON PROBLEM
EXAMPLE 99: MORLEY’S THEOREM
EXAMPLE 100: A LADDER PROBLEM
EXAMPLE 101: AN INSCRIBABLE AND CIRCUMSCRIBABLE PENTAGON

CALCULUS EXPLORATIONS WITH GEOMETRY EXPRESSIONS
HANNAH IRINA LYUBLINSKAYA/ HANNAH VALERIY RYZHIK
INTRODUCTION
CROSS REFERENCE TABLE
1. LIMITS
1.1 THE FORMAL DEFINITION OF A LIMIT
1.2 THE SQUEEZE THEOREM
1.3 AREA OF A CIRCLE
2. DERIVATIVES
2.1 EXPLORING TANGENT LINES
2.2 MEAN VALUE THEOREM
2.3 THE DERIVATIVE OF EVEN FUNCTIONS
2.4 THE DERIVATIVE OF ODD FUNCTIONS
2.5 DIFFERENTIABILITY OF A PIECEWISE FUNCTION AT A POINT
2.6 DERIVATIVE OF AN INVERSE FUNCTION
3. APPLICATIONS OF DERIVATIVES
3.1 ENVELOPE OF A PARABOLA
3.2 LINEAR APPROXIMATION
3.3 NEWTON’S METHOD
3.4 RECTANGLE IN A SEMICIRCLE
3.5 FLOATING LOG
3.6 ART GALLERY
4. INTEGRALS AND THEIR APPLICATIONS
4.1 REPRESENTATION OF THE ANTIDERIVATIVE
4.2 THE FUNDAMENTAL THEOREM OF CALCULUS
4.3 THE SECOND FUNDAMENTAL THEOREM OF CALCULUS
4.4 INTEGRAL OF AN INVERSE FUNCTION
4.5 THE TRAPEZOIDAL METHOD
4.6 MINIMUM AREA
5. DIFFERENTIAL EQUATIONS
5.1 ORTHOGONAL TRAJECTORY TO A CIRCLE
5.2 ORTHOGONAL TRAJECTORY TO A HYPERBOLA
6. SEQUENCES AND SERIES
6.1 INFINITE STAIRS
6.2 THE SNOWMAN PROBLEM
6.3 TRIGONOMETRIC DELIGHT
6.4 CONVERGING OR DIVERGING?
7. PARAMETRIC EQUATIONS AND POLAR COORDINATES
7.1 FOLIUM OF DESCARTES USING PARAMETRIC EQUATIONS
7.2 FOLIUM OF DESCARTES IN POLAR COORDINATES

101 CONIC SECTIONS EXAMPLES WITH GEOMETRY EXPRESSIONS (Philip Todd)
INTRODUCTION
ELEMENTARY EXAMPLES
EXAMPLE 1: TWO PINS AND A PIECE OF STRING
EXAMPLE 2: OPTICAL PROPERTY OF FOCI
EXAMPLE 3: ELLIPSE GIVEN SEMI-MAJOR AND SEMI-MINOR AXES
EXAMPLE 4: HYPERBOLA AS A LOCUS OF CONSTANT DIFFERENCES
EXAMPLE 5: OPTICAL PROPERTIES OF THE HYPERBOLA
EXAMPLE 6: CONJUGATE HYPERBOLAS
EXAMPLE 7: PARABOLA IN TERMS OF FOCUS AND DIRECTRIX
EXAMPLE 8: OPTICAL PROPERTIES OF THE PARABOLA
EXAMPLE 9: GENERAL CONIC VIA FOCUS / DIRECTRIX
EXAMPLE 10: POLAR LINE
EXAMPLE 11: LOCUS OF INTERSECTIONS OF TANGENTS AT THE END OF CHORDS THROUGH A FIXED POINT
PARAMETRIC LOCATION
EXAMPLE 12: PARAMETRIC LOCATION ON AN ELLIPSE
EXAMPLE 13: CONJUGATE DIAMETERS AND PARAMETRIC LOCATION
EXAMPLE 14: HYPERBOLA PARAMETER
EXAMPLE 15: AXIS INTERSECTIONS OF ELLIPSE TANGENTS
EXAMPLE 16: AXIS INTERSECTIONS OF HYPERBOLA TANGENTS
EXAMPLE 17: CONJUGATE DIAMETERS AND HYPERBOLA PARAMETER
EXAMPLE 18: PARAMETRIC LOCATION ON A PARABOLA
ELLIPSE EXAMPLES
EXAMPLE 19: LOCUS OF INTERSECTIONS OF PERPENDICULAR TANGENTS
EXAMPLE 20: LOCUS OF INTERSECTION OF TANGENTS AT THE ENDS OF A CHORD THROUGH THE FOCUS
EXAMPLE 21: ANGLE BETWEEN TWO TANGENTS
EXAMPLE 22: TANGENT DIRECTION
EXAMPLE 23: LOCUS OF MIDPOINTS OF PARALLEL CHORDS
EXAMPLE 24: ANGLE BETWEEN SUPPLEMENTAL CHORDS
EXAMPLE 25: FOCAL TRIANGLE
EXAMPLE 26: LOCUS OF INTERSECTION OF TANGENTS DEFINED BY THE FOCAL TRIANGLE
EXAMPLE 27: TRIANGLE THROUGH CENTER AND FOCUS
EXAMPLE 28: TRIANGLE FORMED BY TANGENT AT END OF DIAMETER, AND FOCAL CHORDS
EXAMPLE 29: PROJECTING THE FOCUS ONTO THE TANGENT
EXAMPLE 30: FOOT OF THE NORMAL
EXAMPLE 31: CENTRAL NORMAL
EXAMPLE 32: LENGTH OF LINE FROM CENTER TO TANGENT PARALLEL WITH FOCAL RADIUS
EXAMPLE 33: LATUS RECTUM
EXAMPLE 34: DISTANCE TO FOCUS AND TO FOCAL TANGENT
EXAMPLE 35: LOCUS OF INTERSECTION OF TANGENT WITH PARALLEL RADIUS THROUGH THE CENTER
EXAMPLE 36: QUADRILATERAL CIRCUMSCRIBING A CENTRAL CONIC
PARABOLA EXAMPLES
EXAMPLE 37: FIND THE CANONICAL FORM OF A PARABOLA
EXAMPLE 38: FINDING THE PARAMETER OF A PARABOLA
EXAMPLE 39: RELATIONSHIP BETWEEN THE LENGTHS OF PERPENDICULAR TANGENTS
EXAMPLE 40: NORMAL AND SUBNORMAL
EXAMPLE 41: PARABOLA TANGENTS
EXAMPLE 42: TANGENT NORMAL AXIS TRIANGLE
EXAMPLE 43: TANGENT INTERSECTION
EXAMPLE 44: LINE JOINING TANGENT INTERSECTION TO FOCUS
EXAMPLE 45: LINE FROM CHORD’S INTERSECTION WITH DIRECTRIX
EXAMPLE 46: CIRCUMCIRCLE OF THREE TANGENT INTERSECTIONS PASSES THROUGH THE FOCUS
EXAMPLE 47: INTERSECTION OF THE FOCUS-TANGENT PERPENDICULAR WITH THE LINE FROM VERTEX TO POINT OF CONTACT
EXAMPLE 48: INTERSECTION OF THE FOCUS-TANGENT PERPENDICULAR WITH THE HORIZONTAL FROM THE POINT OF CONTACT
EXAMPLE 49: ORTHOCENTER OF THE TANGENT TRIANGLE
EXAMPLE 50: AREA OF TANGENT TRIANGLE
EXAMPLE 51: ARCHIMEDEAN TRIANGLES AND QUADRATURE OF A PARABOLA
EXAMPLE 52: LOCUS OF INTERSECTIONS OF TANGENTS OF GIVEN ANGLE
EXAMPLE 53: LOCUS OF THE FOOT OF THE FOCUS-NORMAL PERPENDICULAR
EXAMPLE 54: LOCUS OF INTERSECTION OF PERPENDICULAR NORMALS
EXAMPLE 55: COORDINATES OF THE INTERSECTION OF TWO NORMALS
EXAMPLE 56: A THEOREM OF STEINER’S
EXAMPLE 57: PARAMETRIC QUADRATIC
EXAMPLE 58: HOW TO FIND A PARABOLA’S VERTEX FROM A CHORD AND THE TANGENTS AT ITS ENDS
HYPERBOLA EXAMPLES
EXAMPLE 59: HYPERBOLA WITH GIVEN ASYMPTOTES
EXAMPLE 60: PONCELET BRIANCHON HYPERBOLA PROBLEM
EXAMPLE 61: 9 POINT CIRCLE OF A TRIANGLE INSCRIBED IN A RIGHT HYPERBOLA
EXAMPLE 62: TANGENT INTERSECTIONS WITH ASYMPTOTES
SOME LOCI YIELDING CONICS
EXAMPLE 63: LOCUS OF INCIRCLES
EXAMPLE 64: CIRCLE THROUGH A POINT WITH GIVEN INTERCEPT TO A FIXED LINE
EXAMPLE 65: CIRCLE THROUGH A POINT WHOSE INTERCEPT WITH A GIVEN LINE SUBTENDS A FIXED ANGLE AT THAT POINT
EXAMPLE 66: INTERSECTION OF THE PERPENDICULAR FROM THE CENTER TO A TANGENT WITH THE FOCAL RADIUS
EXAMPLE 67: LOCUS OF INTERSECTION OF TANGENTS AT THE END OF CONJUGATE DIAMETERS
EXAMPLE 68: INTERSECTION OF NORMALS AT ENDS OF FOCAL CHORD
EXAMPLE 69: LOCUS OF INTERSECTION OF DIAGONALS OF A TRAPEZIUM
EXAMPLE 70: LOCUS OF CENTER OF SEGMENT OF TANGENT CUT OFF BY TWO FIXED TANGENTS
EXAMPLE 71: NEWTON’S CONIC CONSTRUCTION
EXAMPLE 72: MACLAURIN’S CONIC CONSTRUCTION
SOME EXAMPLES INVOLVING ENVELOPES
EXAMPLE 73: ENVELOPE OF HYPOTENUSE OF RIGHT ANGLED TRIANGLE, WHOSE SHORT SIDES ADD UP TO A CONSTANT
EXAMPLE 74: ENVELOPE OF HYPOTENUSE OF RIGHT ANGLED TRIANGLES OF CONSTANT AREA
EXAMPLE 75: A TRIANGLE WHOSE VERTICES TRAVERSE FIXED LINES AND TWO OF WHOSE SIDES PASS THROUGH FIXED POINTS
EXAMPLE 76: ENVELOPE OF HYPOTENUSE OF RIGHT ANGLED TRIANGLES WITH CONSTANT PERIMETER
EXAMPLE 77: THE ENVELOPE OF THE LINE THE PRODUCT OF WHOSE DISTANCES FROM TWO FIXED POINTS IS CONSTANT
EXAMPLE 78: A LINE AT FIXED ANGLE TO A SEGMENT FROM A FIXED POINT TO A FIXED LINE
EXAMPLE 79: CROSS SECTION OF A HYPERBOLOID
EXAMPLE 80: SIDES OF REFLECTED TRIANGLE
CENTERS OF CURVATURE, EVOLUTES AND CAUSTICS
EXAMPLE 81: CENTERS OF CURVATURE OF AN ELLIPSE
EXAMPLE 82: RADIUS OF CURVATURE IN TERMS OF NORMAL AND SEMI-PARAMETER
EXAMPLE 83: CENTERS OF CURVATURE OF A HYPERBOLA
EXAMPLE 84: CENTERS OF CURVATURE OF A PARABOLA
EXAMPLE 85: FOCAL CHORD OF CURVATURE A PARABOLA
EXAMPLE 86: CONSTRUCTION FOR CENTER OF CURVATURE OF AN ELLIPSE
EXAMPLE 87: EVOLUTE EQUATION OF A PARABOLA
EXAMPLE 88: PARABOLA CAUSTIC WITH INCOMING LIGHT PERPENDICULAR TO THE AXIS
EXAMPLE 89: PARABOLA CAUSTIC FROM PARALLEL RAYS SKEW TO THE AXIS
SYNTHETIC METHODS
EXAMPLE 90: AXIS INTERSECTIONS OF A CONIC
EXAMPLE 91: EQUATION OF THE CONIC THROUGH FIVE GIVEN POINTS
EXAMPLE 92: FAMILY OF CONICS WHICH INTERSECT A GIVEN CONIC IN THE SAME POINTS AS A PAIR OF LINES
EXAMPLE 93: CONIC MAKING DOUBLE CONTACT WITH A GIVEN CONIC
EXAMPLE 94: CONIC GIVEN TWO TANGENTS AND CHORD OF CONTACT
PAIRS OR FAMILIES OF CONICS
EXAMPLE 95: CONFOCAL CONICS INTERSECT AT RIGHT ANGLES
EXAMPLE 96: A LINE CUTTING TWO SIMILAR CONCENTRIC CONICS
EXAMPLE 97: ANGLE BETWEEN TANGENTS TO AN INNER AND OUTER CONCENTRIC SIMILAR ELLIPSE
EXAMPLE 98: LOCUS OF TANGENT POINTS TO A FAMILY OF CONFOCAL CONICS
EXAMPLE 99: POINT OF CONTACT OF CONFOCAL CONIC TANGENT TO A FAMILY OF PARALLEL LINES
EXAMPLE 100: POINT OF CONTACT OF CONIC TANGENT TO A FAMILY OF LINES PASSING THROUGH A POINT ON THE AXIS
EXAMPLE 101: LOCUS OF CENTERS OF CONICS WHICH PASS THROUGH A TRIANGLE AND ITS ORTHOCENTER

CONNECTING ALGEBRA AND GEOMETRY THROUGH TECHNOLOGY JIM WIECHMANN
INTRODUCTION
PROFESSIONAL DEVELOPMENT UNIT FOR GEOMETRY EXPRESSIONS USING
A CONSTRAINT APPROACH IN TEACHING MATHEMATICS
INTRODUCTION
GUIDE TO THE SCREEN
LESSON 1: USING THE CONSTRAINT APPROACH
LESSON 2: DRAWING GEOMETRIC FIGURES
LESSON 3: SYMBOLIC OUTPUTS AND REAL OUTPUTS
LESSON 4: VARIATION AND ANIMATION
LESSON 5: FUNCTIONS AND LOCI
APPENDIX: TROUBLESHOOTING
APPLYING GEOMETRY EXPRESSIONS IN THE ALGEBRA 2 AND PRE-CALCULUS CLASSROOMS
UNIT 1: PARAMETRIC FUNCTIONS
LESSON 1: A QUICK REVIEW OF FUNCTIONS
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 2: DUDE, WHERE’S MY FOOTBALL?
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 3: GO SPEED RACER!
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 4: PARAMETRIC PROBLEMS
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
UNIT 2: CONICS AND LOCI
LESSON 1: INTRODUCING LOCI
LEARNING OBJECTIVES
STUDENT WORKSHEETS
LESSON 2: THE CIRCLE
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 3: THE ELLIPSE
LEARNING OBJECTIVES
STUDENT WORKSHEETS
LESSON 4: CONICS AND ENVELOPE CURVES
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 5: INSIDE OUT ELLIPSES
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 6: ECCENTRICITY
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS

DEVELOPING GEOMETRY PROOFS WITH GEOMETRY EXPRESSIONS™
IRINA LYUBLINSKAYA, VALERIY RYZHIK, DAN FUNSCH
I. INTRODUCTION
II. HOW TO USE THESE MATERIALS
CROSS REFERENCE TABLE
III. DESCRIPTION OF PROOF METHODS
GEOMETRIC METHOD
1. SEGMENTS IN A SQUARE – PURE GEOMETRY
ALGEBRAIC METHOD
2. SEGMENTS IN A SQUARE – ALGEBRA FOR ALL
COORDINATE METHOD
3. SEGMENTS IN A SQUARE – ON A COORDINATE PLANE
VECTOR METHOD
4. SEGMENTS IN A SQUARE – FOLLOW THE VECTOR
TRANSFORMATIONS METHOD
5. SEGMENTS IN A SQUARE – NEW SPIN!
IV. RELATIONSHIPS BETWEEN GEOMETRIC FIGURES
COLLINEARITY
6. DIAMETER OF A CIRCLE
7. ANGLE BISECTORS OF A TRAPEZOID
PARALLELISM
8. EXTERIOR ANGLE BISECTOR
PERPENDICULARITY
10. TWO INTERSECTING CIRCLES
11. TWO ANGLE BISECTORS
TYPES OF GEOMETRIC FIGURES
12. TWO TANGENT CIRCLES
13. IT’S A TRAPEZOID
14. SHAPE OF A QUADRILATERAL
15. QUADRILATERAL IN A TRAPEZOID
17. RECTANGLES WITH EQUAL AREAS
18. SLIDING SEGMENT
19. UNEXPECTED LOCUS
V. RELATIONSHIPS BETWEEN MEASURES OF GEOMETRIC FIGURES
SEGMENT LENGTH
20. LENGTH OF A COMMON TANGENT
21. TWO MEDIANS IN A TRIANGLE
22. INSCRIBED TRAPEZOID
23. TWO CONCENTRIC CIRCLES
24. RIGHT TRIANGLE INEQUALITY
25. DIAGONAL OF A PARALLELOGRAM
26. SEGMENT IN A TRIANGLE
27. POINT INSIDE AN EQUILATERAL TRIANGLE
28. TRIANGLE WITH THE SMALLEST PERIMETER
29. POWER OF A POINT THEOREM
30. SHORTEST PATH
31. TWO EQUAL CIRCLES
AREA
32. AREA OF A QUADRILATERAL
33. QUADRILATERAL IN A SQUARE
34. AREA COMPARISON
35. TRIANGLE IN A SQUARE
36. TRIANGLE WITH THE LARGEST AREA
ANGLE
37. SEGMENTS IN AN EQUILATERAL TRIANGLE
38. STAR259
39. ANGLE COMPARISON
VI. RECONSTRUCTION PROBLEMS
40. TRIANGLE FROM THREE MIDPOINTS
41. RESTORING AN EQUILATERAL TRIANGLE
42. TRIANGLE FROM THREE MEDIANS
43. FROM TRAPEZOID TO SQUARE
VII. CONCLUSION

EXPLORING WITH GEOMETRY EXPRESSIONS IN HIGH SCHOOL MATHEMATICS IAN SHEPPARD
CHAPTER 1 – INTRODUCTION
CHAPTER 2 – CONSTRAINTS
CHAPTER 3 – ALGEBRA IN GX (SYMBOLICS)
CHAPTER 4 – DANNY’S ROOM
CHAPTER 5 – CONGRUENCE
LAB # 1 THREE SIDES
LAB # 2 TWO SIDES AND AN ANGLE
LAB # 3 HYPOTENUSE AND A SIDE
LAB # 4 TWO ANGLES AND A SIDE
LAB # 5 THREE ANGLES
CHAPTER 6 – PROOF
LAB # 6 CONGRUENT TRIANGLES - SSS
LAB # 7 BISECT AN ANGLE
LAB # 8 CONSTRUCT A PARALLEL LINE 46
LAB # 9 COPY AN ANGLE
LAB # 10 PERPENDICULAR BISECTOR
LAB # 11 CENTRAL ANGLE THEOREM
LAB # 12 OTHER CIRCLE THEOREMS
LAB # 13 THE “CENTER” OF A TRIANGLE
CHAPTER 7 – SLIDE, TURN, FLIP, AND RESIZE
LAB # 14 SLIDE
LAB # 15 CLIMBING UP!
LAB # 16 SLIDING WITH COORDINATES
LAB # 17 TURN RIGHT
LAB # 18 TURNING WITH COORDINATES
LAB # 19 FERRIS WHEEL
LAB # 20 FLIPPING OVER
LAB # 21 MULTIPLE FLIPS
LAB # 22 KALEIDOSCOPE
LAB # 23 FLIPPING AND COORDINATES
LAB # 24 RESIZE
LAB # 25 RESIZE AND COORDINATES
LAB # 26 DETERMINING THE DILATION
CHAPTER 8 – RIGHT INTO TRIANGLES
LAB # 27 PYTHAGOREAN THEOREM
LAB # 28 CONVERSE OF THE PYTHAGOREAN THEOREM
LAB # 29 RIGHT TRIANGLES - 30° AND 45°
LAB # 30 MEASURES OF “STANDARD” TRIANGLES
LAB # 31 USE OF SIMILAR TRIANGLES TO SOLVE RIGHT TRIANGLES
LAB # 32 TARGET PRACTICE
LAB # 33 SINE FORMULA
LAB # 34 LAW OF COSINES
LAB # 35 SOLVING NON-RIGHT TRIANGLES
LAB # 36 HOW MUCH HIGHER?
LAB # 37 STRANDED ON AN ISLAND
LAB # 38 DISTANCE FORMULA
LAB # 39 MIDPOINT FORMULA
LAB # 40 MIDPOINTS OF A QUADRILATERAL
LAB # 41 DIAGONALS OF A RHOMBUS
LAB # 42 ANGLE IN A SEMICIRCLE
LAB # 43 THE LAW OF COSINES
LAB # 44 SUBTRACTION FORMULA

CHAPTER 10 – LOCI
LAB # 45 THE CIRCLE
LAB # 46 SHAKE IT MAMA
LAB # 47 DISTANCE FROM TWO POINTS
LAB # 48 DETECTIVE WORK?
LAB # 49 TURKEY TETHER
LAB # 50 PARABOLIC FOCUS
LAB # 51 BEZIER CURVES
REFERENCES
APPENDIX A – GX AND FUNCTIONS
APPENDIX B - INSIGHT WITH GEOMETRY EXPRESSIONS
INTRODUCTION
WARM UP
A SEQUENCE OF ALTITUDES
ANGLES AND CIRCLES
TRIANGULATION
RECTANGLE CIRCUMSCRIBING AN EQUILATERAL TRIANGL
AREA OF A HEXAGON BOUNDED BY TRIANGLE SIDE TRISECTORS
AN INVESTIGATION OF INCIRCLES, CIRCUMCIRCLES AND RELATED MATTERS
CIRCUMCIRCLE RADIUS
INCIRCLE RADIUS
INCIRCLE CENTER IN BARYCENTRIC COORDINATES
HOW DOES THE POINT OF CONTACT WITH THE INCIRCLE SPLIT A LINE?
EXCIRCLES
THE PROGRAM IS CAREER APPLICATION IN MULTIPLE AREA TO ALL PROFESSIONAL
| |
| FUNCTION TRANSFORMATIONS TIM BROWN | |
| USING SYMBOLIC GEOMETRY TO TEACH SECONDARY SCHOOL MATHEMATICS - GEOMETRY EXPRESSIONS ACTIVITIES FOR ALGEBRA 2 AND PRECALCULUS IRINA LYUBLINSKAYA, VALERIY RYZHIK | |
| THE FARMER AND THE MATHEMATICIAN: USING GEOMETRY EXPRESSIONS™ AND GOOGLE™ EARTH TO INVESTIGATE CROP CIRCLES - I LARRY OTTMAN | |
| THE FARMER AND THE MATHEMATICIAN: USING GEOMETRY EXPRESSIONS™ AND GOOGLE™ EARTH TO INVESTIGATE CROP CIRCLES - II LARRY OTTMAN | |
THE TORTOISE AND ACHILLES USING GEOMETRY EXPRESSIONS™ TO INVESTIGATE THE INFINITE LARRY OTTMAN | |
ATLAS OF THE FOUR-BAR LINKAGE EUGENE FICHTER, PHILIP TODD, DIETER MUELLER |
FUNCTION TRANSFORMATIONS TIM BROWN
INTRODUCTION
UNIT 1: INTRODUCTION TO TRIGONOMETRY
LESSON 1: RIGHT TRIANGLE TRIGONOMETRY
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 2: THE UNIT CIRCLE
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
UNIT 2: FUNCTION TRANSFORMATIONS
LESSON 1: VERTICAL TRANSLATIONS OF FUNCTIONS
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 2: VERTICAL DILATIONS
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 3: COMBINED VERTICAL TRANSFORMATIONS
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 4: CIRCULAR AND HARMONIC MOTION
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 5: HORIZONTAL AND COMBINED TRANSFORMATIONS
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
LESSON 6: SINUSOIDAL CURVES
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
EXTENSION A: CIRCLES AND ELLIPSES
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
EXTENSION B: ABSOLUTE VALUE
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
EXTENSION C: COSINE AND TANGENT
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS
EXTENSION D: VERTICAL ASYMPTOTES
LEARNING OBJECTIVES
OVERVIEW FOR THE TEACHER
STUDENT WORKSHEETS

USING SYMBOLIC GEOMETRY TO TEACH SECONDARY SCHOOL MATHEMATICS - GEOMETRY EXPRESSIONS ACTIVITIES FOR ALGEBRA 2 AND PRECALCULUS IRINA LYUBLINSKAYA, VALERIY RYZHIK
INTRODUCTION
DISCOVERING PARABOLAS
PART 1 – PARABOLA BY 3 POINTS
PART 2 – THE EXISTENCE OF A PARABOLA PASSING THROUGH THREE ARBITRARY POINTS
EXTENSIONS:
SOLVING SYSTEMS OF EQUATIONS (INEQUALITIES) WITH PARAMETERS
PART 1 – SETTING UP THE PROBLEM IN GEOMETRY EXPRESSIONS
PART 2 – WHEN THE SYSTEM HAS NO SOLUTIONS
PART 3 – INVESTIGATION OF THE NUMBER OF SOLUTIONS
PART 4 – SOLVING SYSTEMS OF EQUATIONS
PART 5 – SOLVING SYSTEMS OF INEQUALITIES WITH PARAMETERS
EXTENSIONS:
STAINED GLASS DESIGN
PART 1 – SETTING UP PROBLEM IN GEOMETRY EXPRESSIONS
PART 2 – CREATING STAINED GLASS DESIGN
PART 3 – FINDING EQUATIONS OF THE CURVES IN THE STAINED GLASS DESIGN
PART 4 – VERIFICATION OF THE EQUATIONS WITH GEOMETRY EXPRESSIONS
EXTENSIONS
TRANSLATION ALONG COORDINATE AXES
PART 1 – TRANSLATION ALONG THE Y-AXIS
PART 2 – TRANSLATION ALONG THE X-AXIS
PART 3 – COMMUTATIVE PROPERTY OF TRANSLATION
PART 4 – APPLICATIONS AND ASSESSMENT PROBLEMS
EXTENSION:
A LITTLE TRIG
PART 1 – INVESTIGATING AREA OF THE TRIANGLE
PART 2 – OPTIMIZING THE PERIMETER OF THE RECTANGLE
ONE HYPERBOLA
PART 1 – INVESTIGATING AREA OF THE RECTANGLE
PART 2 – OPTIMIZING PERIMETER OF THE RECTANGLE
PART 3 – OPTIMIZATION OF THE DIAGONAL OF THE RECTANGLE
THREE EXTREMA (CIRCLE)
PART 1 – LENGTH OF A TANGENT SEGMENT TO A CIRCLE
PART 2 – AREA OF A TRIANGLE FORMED BY A TANGENT LINE AND THE COORDINATE AXES
PART 3 – PERIMETER OF A RECTANGLE WHOSE DIAGONAL IS A TANGENT SEGMENT
TWO PARABOLAS
PART 1 – OPTIMIZING PERIMETER OF RECTANGLE
PART 2 – OPTIMIZING THE DIAGONAL OF THE RECTANGLE
PART 3 – COMPARISON OF POINTS OF EXTREMA FOR PERIMETER, DIAGONAL, AND AREA

THE FARMER AND THE MATHEMATICIAN: USING GEOMETRY EXPRESSIONS™ AND GOOGLE™ EARTH TO INVESTIGATE CROP CIRCLES LARRY OTTMAN
LESSON ONE
QUICK QUESTIONS
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
LESSON TWO
QUICK QUESTIONS
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
LESSON THREE: THE ALGEBRA FARMER
QUICK QUESTIONS
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
LESSON FOUR
QUICK QUESTIONS
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
EXCITING EXTENSIONS
DRAMATIC DIVERSION
LESSON FIVE
QUICK QUESTIONS
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
EXCITING EXTENSION
LESSON SIX: THE ALGEBRA FARMER II
INFORMATIVE INSTRUCTIONS
LESSON SEVEN
QUICK QUESTIONS
INFORMATIVE INSTRUCTIONS
TABLE OF CONTENTS
REPORTING RESULTS
EXCITING EXTENSION
LESSON EIGHT
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
EXCITING EXTENSION
EXHILARATING EXTENSION
TAXING TRIGONOMETRIC TREK
LESSON NINE: THE GREEDY FARMER
INFORMATIVE INSTRUCTIONS
REPORTING RESULTS
TEACHER NOTES
INTRODUCTION
OBJECTIVES
LESSON ONE
LESSON NOTES
OBJECTIVES
LESSON TWO
LESSON NOTES
LESSON THREE
LESSON NOTES
OBJECTIVES
LESSON FOUR
LESSON NOTES
OBJECTIVES
LESSON FIVE
LESSON NOTES
LESSON SIX
OBJECTIVES
LESSON NOTES
OBJECTIVES
LESSON SEVEN
LESSON NOTES
LESSON EIGHT
OBJECTIVES
LESSON NOTES
LESSON NINE
OBJECTIVES
LESSON NOTES
FURTHER INVESTIGATION

THE FARMER AND THE MATHEMATICIAN: USING GEOMETRY EXPRESSIONS™ AND GOOGLE™ EARTH TO INVESTIGATE CROP CIRCLES II LARRY OTTMAN
The Farmer is back and he’s been collecting a lot of questions for his new mathematician. (The mathematician from our last book is “on vacation - practicing his zero slope!”) Our farmer is still using his Center Pivot Irrigation System – those long stretches of wheeled scaffolding, sometimes up to a half mile in length, rotating around a fixed point attached to his water source. And he’s become quite good at scanning Google Earth to see what his fellow farmers are up to.
Again, as in the first book, The Farmer and the Mathematician, we demonstrate to the student that Mathematics is not just for calculating the price of produce in
the grocery store. Here we have a fresh batch of examples of mathematics in action using our symbolic geometry software, Geometry Expressions, with
images from Google Earth.
The process of mathematical modeling is both critical to using mathematics in the world around us, and to developing an understanding and appreciation for the
true utility of mathematics. A mathematician or engineer would first be given a problem to solve. They would also be given constraints, or a set of rules
and conditions that must be followed. From that, the scientist would attempt to create a mathematical representation of the problem. Often, real problems are
much too complex and it is necessary to constrain, or simplify them further. This is very similar to the approach that a student would take to gain insight into a
problem by solving a simpler, related one. Geometry Expressions has been written to mirror this process. It is a constraint-based geometric and algebraic
modeling program that allows the student to investigate problems in both a numeric and symbolic representation.
So join the Farmer and his mathematical instructor, Sophie, as they fly over Texas, investigating interesting geometrical ideas and stumbling over important
mathematical concepts. The content is appropriate and adaptable for students in a range of courses from Algebra and Geometry up through and including
Calculus.

THE TORTOISE AND ACHILLES USING GEOMETRY EXPRESSIONS™ TO INVESTIGATE THE INFINITE LARRY OTTMAN
LESSON ONE
LESSON TWO
LESSON THREE
LESSON FOUR
LESSON FIVE
LESSON SIX
LESSON SEVEN
LESSON EIGHT
LESSON NINE
LESSON TEN
TEACHER NOTES
LESSON ONE
LESSON
TWO LESSON
THREE LESSON
FOUR LESSON
FIVE LESSON
SIX LESSON
SEVEN LESSON
EIGHT LESSON
NINE LESSON
TEN LESSON

ATLAS OF THE FOUR-BAR LINKAGE EUGENE FICHTER, PHILIP TODD, DIETER MUELLER
1. INTRODUCTION
THERE ARE MANY SITUATIONS IN MACHINE DESIGN WHICH REQUIRE PARTS TO MOVE ALONG COMPLEX PATHS. CAMS AND LINKAGES ARE TWO COMMONLY USED DEVICES FOR PRODUCING SUCH MOVEMENT. EACH OF THESE DEVICES HAS ADVANTAGES AND DISADVANTAGES, BUT FOR MANY DESIGNS THE ADVANTAGES OF A LINKAGE ARE SUBSTANTIAL IF THE DIFFICULTY OF DESIGNING THE LINKAGE CAN BE OVERCOME. THE OBJECTIVE OF THIS ATLAS IS TO SIMPLIFY THE TASK OF DESIGNING FOUR-BAR LINKAGES WITH EITHER PIN JOINTS OR SLIDERS
2. CRANK ROCKER
3. CRANK CRANK
4. CRANK SLIDER
5. INVERTED CRANK SLIDER