UM Experiments
UM Experiments
Introduction - scanning, optimization, approximation - Scanning distributed calculations - Optimization - Approximation - Analytic hierarchy process - Service of distributed calculations
Introduction
It is often required in engineering practice to carry out series of numerical experiments, for example to analyze dynamical behavior and sensitivity of mechanical system or to find out optimal parameters of the system. The built-in module UM Experiments includes a set of tools (scanning, optimization, approximation), for advanced analysis of dynamics of mechanical systems.
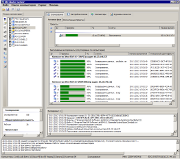
All tools automate fulfillment of series of numerical experiments, record course of experiments and save results of experiments on a hard disk for posterior analysis. Thus, the designer is released from monotonous execution of series of numerical experiments "manually" what saves working hours and removes errors, which people unfortunately incline to do. In other words, the researcher defines the design of experiments for scanning and approximation or parameters, its limits and precision and goal function for optimization. Then the project is started and executed automatically. Current process statistics is available during the execution: number of experiments done, time left. Series of numerical experiments are resistant to shut-down of power supply. In that case all results are saved on a hard disk and results of the latter experiments are only lost. There is a possibility to plot an oscillogram of any saved performance of dynamical behavior of a mechanism. Moreover, the designer can plot so-called summary graphs and surfaces. All implemented tools have no limitation in number of parameters. In other words, they all are multi-parametrical. Please, note that the demo version allows describing the projects of scanning (optimization, approximation) with no more than one parameter. Dimensions of projects are set by the designer so as to solve the specify problem. But on the other hand the designer has to take into account calculating efforts that are necessary for the project. Every tool has its own merits and demerits. However they all give the designer possibilities to solve quite many problems devoted to optimization of mechanical systems.
After the execution of series of numerical experiments for scanning the problem of choosing the optimal parameters arises. How can the designer find out the best solution from lots of alternatives? It becomes much more difficult in the case of conflicting criteria. In order to help the designer to formalize her/his opinion the special tool, which helps the designer to sort alternatives according to her/his opinion about optimality, was developed. This tool is based on the analytic hierarchy process by Tomas L. Saaty. It is a multi-criteria method, which supports weighting of criteria, conflicting criteria and verification of correctness of experts opinion.
There is a special extension of the module - service of distributed calculations. It allows using all computational powerful of a network for execution of series of numerical experiments that decreases time efforts correspondingly. This possibility is very easy and effective to use in computer centers and laboratories. Server of distributed calculations is based on using TCP/IP that allows employing any computer not only in local network, but also in Intra- and Internet for the needs of your project.
Scanning
Designer describes parameters to scan (as a rule, it is geometrical, inertia, stiffness and damping parameters), limits and step size for each parameter and starts series of numerical experiments. Scanning saves time history of all selected dynamical performances on a hard disk. These performances are available after the execution of the project. There are special possibilities for scanning dynamical behavior of railway vehicles: with various rail and wheel profiles, various tracks (tangent tracks and curves), various railway track irregularities. Scanning gives us full information about the response surface and the global optimum. It is usually enough to solve an optimization problem. On the other hand, scanning is very time-consuming process so as it is not practically used for problems with dimension more than 4-5. Scanning supports service of distributed calculations that decreases time efforts considerably.
Optimization
This tool is based on a number of classical optimization methods: Hook-Jeevse,s, Nealder-Mead,s, Pawell,s etc. The advantage of this tool is quite low computational efforts. On the other hand the tool has some disadvantages. Firstly, there is always a possibility that the method stops in one of the local optimums and does not find the global one. Secondly, all what the designer has after this kind of optimization does not give the shape of the objective function, it gives just several points on it. So the designer cannot get general overview of the dynamical behavior of the system. However it is well-known that objective functions of real mechanical systems are quite smooth, otherwise it would be high parameter sensitivity of the system that should not take place in real systems.
Approximation
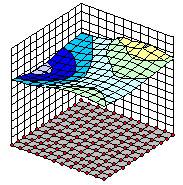
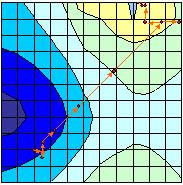
The designer describes parameters and its limits too. Unlike scanning, the numerical experiments are calculated for several key points in parameter space. Values of objective function in other points are calculated with the help of methods based on quadratic approximation. So this tool leads to extremely low calculation efforts especially for multi-dimensional problems and gives response surface. However there are restrictions on using this approach. Response surface should be smooth and should be represented well with the help of quadratic functions. In fact, these restrictions are not so strong for real technical objects because they normally have smooth and nearly quadratic response surface. Response surfaces calculated as result of scanning and approximation are shown. Maximal relative error is at most 3 % in that example. Practice of modeling shows that, as a rule, maximal relative errors are less than 10-15 %, but time efforts are decreased in several times. However the optimal solution obtained with the help of this approach can be far enough from the true optimum. Generally, this tool is not intended for searching optimum of objective function. It is rather intended for first, fast and actually not so deep overview of dynamical properties of a mechanical system.
Analytic hierarchy process
The analytic hierarchy process was developed by Saaty. Detailed information is available in [1]. The method is based on principle of hierarchization, where the main, most common goal consists of several more detailed sub-goals, each sub-goal of the first level consists of the corresponding sub-goals of level two and so on. Every sub-goal has only one upper goal. Different sub-goals affect the upper goal with a different weight.
Further, the analytic hierarchy process involves the method to determine the weight with which the various elements in one level influence the elements on the next higher level, so that we may compute the relative weight of the impacts of the elements of the lowest level on the overall objectives. The method can be described as follows. Given one goal, and its sub-goals of the next level lower, compare the sub-goals pairwise in their weight of influence on upper level. Let us arrange the agreed upon numbers reflecting the comparison in a matrix and find the eigenvector with the largest eigenvalue. The eigenvector provides the priority ordering, and the eigenvalue is a measure of the consistency of the judgment. To insert the agreed upon numbers the designer has to compare every pair of sub-goals and give an answer for the question "how stronger the influence of sub-goal B on the upper goal than the influence of sub-goal C on it", this number will be included in the (B, C) matrix element. If B and C are equally important then the number is 1, if B is weakly more important than C then the number is 3 and so on up to number 9 when the B is absolutely more important than C. [1].
Saaty, T. The Analytic Hierarchy Process, McGraw-Hill, 1980.
Service of distributed calculations
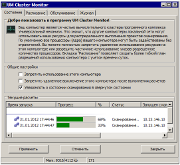
The service is based on TCP/IP protocol. It allows using any computer reachable by TCP/IP under Windows 98/NT/2000/XP for parallel numerical experiments. Service of distributed calculations consists of two parts: server and client ones. The server part works on the head computer and controls the execution, sends jobs and receives results back. The client part is run on the peripheral computers, gets and fulfils jobs and sends results to the server.
Service of distributed calculations runs dozens of numerical experiments of the scanning project simultaneously on other computers that are available in your local network, corporate network or Internet. It significantly decreases total time of completion the project. Service of distributed calculations consists of client and server parts. There might be arbitrary number of computer with installed UM client and/or server parts.
Remote install and uninstall of the client parts on client computers are supported. Remote installation runs automatically without disturbing remote users. There is a built in tool to determine all computers in your local network that simplify initial procedures of searching and adding the client computer.
Server part sends new tasks for remote client computers, controls all stages of running every experiments (including sending the task, running the task and getting simulation results) and the whole scanning project. UM server of distributed calculations can turn on and off remote computers.
Client part has simple and user-friendly tools that give the user a possibility to control remote using his/her computer as a client computer for UM service of distributed calculations. User on the client computer can change the count of CPU cores dedicated for running UM server’s tasks and finally forbid the remote server to use the local computer as a client of UM service of distributed calculations.