UM Wheel-Rail Wear
Introduction
Module UM Wheel/Rail Wear is intended for simulation of wheel and rail wear [1]. The wear of railway wheel and rail profiles is a fundamental problem in railway industry. Many research works have been performed on the prediction of the evolution of wheels and rails due to wear using numerical simulation. Such kind of studies implies using complete models of the railway vehicle/track interaction dynamics, wheel/rail contact and wear. The methodology of the evolution of wheel and rail profiles due to wear consists of the selection of an appropriate set of experiments, the simulation of the railway vehicle/track interaction dynamics, and updating profiles according to using wear model.
Set of experiments
The parameters of set of experiments specify operational conditions of the investigated object. In other words, for the prediction of wear of railway vehicle wheel profiles they could be different track sections (tangents, curves and switches), velocity values, rail profiles, track irregularities and so on. Weighting coefficients should be assigned for the parameters. So the set of experiments should properly coincide with real operational conditions of the considered vehicle. In UM, set of experiments is created by using multivariant calculations (UM Experiments module).
Simulation of railway vehicle/track interaction dynamics
In UM, a three-dimensional multibody model of any railway vehicle can be developed as well as any railway track including tangents, curves, and switches can be created. To obtain reliable results of railway dynamics simulation and the prediction of wheel and rail wear it is necessary to use adequate wheel/rail contact models.
Contact models
The well-known FASTSIM algorithm [2] in which the contact patch is supposed to be elliptical.
The non-elliptical wheel-rail contact model [3] where the elastic Winkler foundation model is used to find the contact patch and the distribution of the normal pressure.
Two contact models are implemented in UM and could be used for the solution of wheel/rail contact problem:
Wear models and profile updating
The parameters calculated by contact models such as stress distributions and slips are used in wear models to calculate the material removal of profiles. Several wear models are realized in UM - Archard model [4] - Specht model - VNIIZhT-1 model - Plasticity model
Two approaches for wear simulation
The process of the simulation of the wheel and rail profile evolution due to wear can be organized in two different ways [5]:
- Sequential approach. In this case, the first step is the simulation of the railway vehicle dynamics and the accumulation of wear for all cases from set of experiments. The second step is updating profiles according to the accumulated wear. Such wear iterations are repeated until the desired wear is obtained.
- Parallel approach. The simulation of vehicle dynamics and the evolution of profiles go on simultaneously. The profile updating is performed during the simulation in some very short time intervals and after the simulation continues with new profiles.
As a rule, the maximal material removal in the process of profile evolution is limited by values about 0.1 mm to obtain rather smooth profiles without “digging holes”. Therefore computing high worn profiles by using the sequential approach demands hundreds and even thousands of wear iterations. For detailed sets of experiments with many parameters and complicated railway vehicle models it requires days of computational time. The parallel approach allows obtaining high worn profiles much faster, but this approach is not as flexible and stable as the sequential one. Both these approaches are realized in UM.
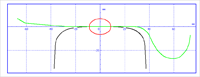
Applications
The first example is the simulation of mutual wear of wheels of a freight car and rails in the curve R = 300 m. The sequential approach with 80 wear iterations was implemented for this simulation. In figures, the wheel and rail profiles as well as typical contact patches, which are calculated with the help of the non-elliptical contact model, for 1, 20, 40 and 80 iterations are shown. One can see that for the initial profiles the contact patches are very close to elliptical. In the sequel contact patches differ from elliptical ones more and more and contact becomes conformal during the simulation.
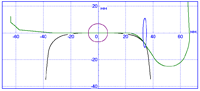
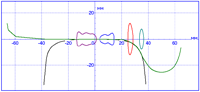

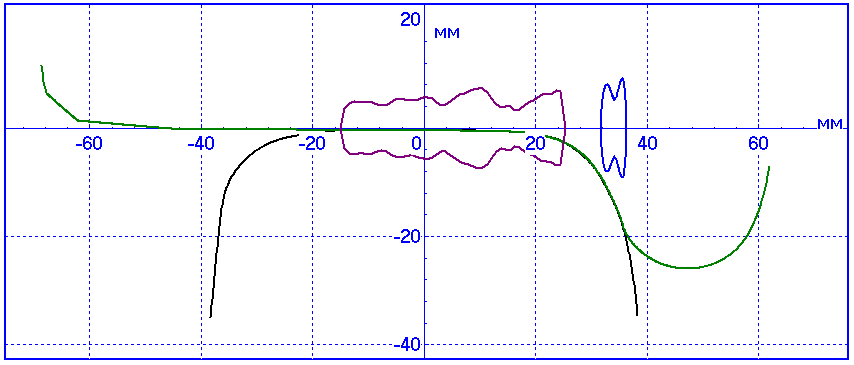
Rail wear
The Example of rail profile wear calculation in curve R="300." Total number of iteration is 204. Every tenth and last rail profiles
References
1. Sergey Zakharov, Irina Goryacheva, Victor Bogdanov, Dmitry Pogorelov, Ilya Zharov, Vladislav Yazykov, Elena Torskaya, Sergey Soshenkov. Problems with wheel and rail profiles selection and optimization. Wear, Vol. 265 (2008), Issues 9-10. – pp. 1266-1272.
2.J.J. Kalker: Three-Dimensional Elastic Bodies in Rolling Contact, Kluwer Academic Publishers, Dordrecht, (1990).
3.R. Kovalev, V.N. Yazykov, G.S. Mikhalchenko, D.Yu. Pogorelov: Railway Vehicle Dynamics: Some Aspects of Wheel-Rail Contact Modeling and Optimization of Running Gears, Mechanics Based Design of Structures and Machines, 31(3), pp. 315–335, (2003).
4.J.F. Archard: Contact and Rubbing of Flat Surface, J. Appl. Phis., 24, pp. 981–988, (1953).
5.J. Piotrowski, W. Kik: A simplified model of wheel/rail contact mechanics for non-Hertzian problems and its application in rail vehicle dynamic simulations, Vehicle System Dynamics, 46 (1), pp 27–48, (2008).




